- ホーム
- NEW
- ほっこりイラスト▼
- 季節の工作等▼
- ひと息 写真集▼
- 生き物図鑑▼
- 和みKANSAI▼
- 花と実図鑑▼
- 頭の体操
- 料理(ごはん)▼
- 月ごと絵手紙▼
頭の体操「つるかめ算」
小学生の難問に挑戦!
では早速、典型的なツルとカメの例題を考えながら、やわらか頭を目指しましょう。
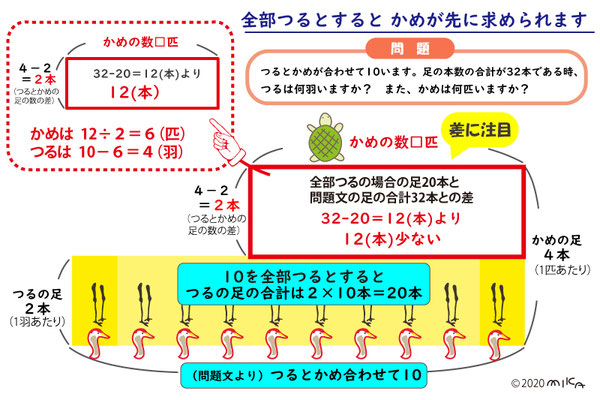
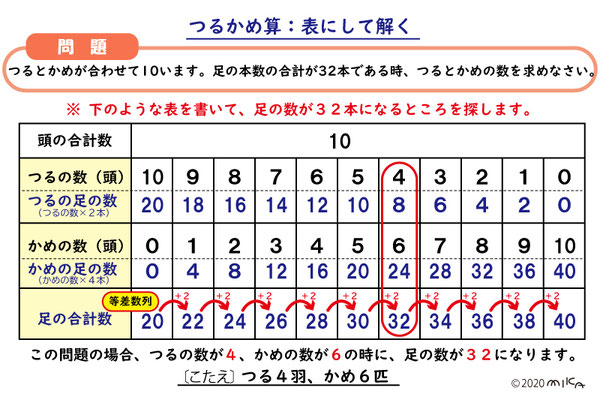
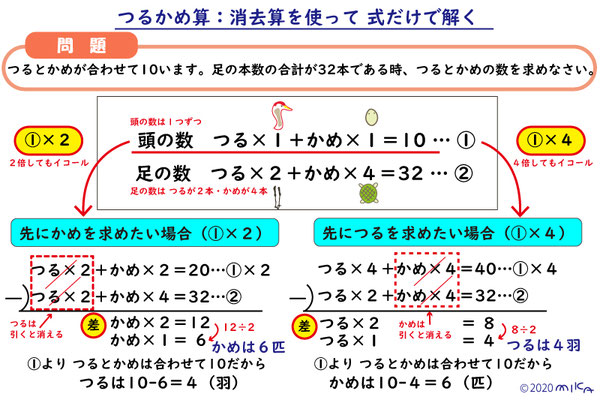
【問題】つるとかめが合わせて10います。足の本数の合計が32本である時、つるは何羽?かめは何匹?
※いろいろな解法がありますが、小学生は連立方程式を使わずに解きますので、他の解法からご紹介します。
1.面積図の利用
長方形の面積を使った つるかめ算の代表的な解法です。たてを1羽(1匹)あたりの足の数、横を頭の数(個体数)として、長方形を書き、長方形の面積が「全部の足の数(足の総数)」を表します。
※つるかめ算のポイントは、「全部がつるだったら…」または「全部がかめだったら…」と仮定して、足の差に注目することです。つるを求めたい時は、全部をかめにし、逆に、かめを求めたいときは、全部をつるにします。
3.取りかえの考え方
これは、面積図は使いませんが、いったん、全部をつる(またはかめ)と考え、足の総数が合うまで、1匹ずつかめ(またはつる)に取り換えていく方法で、式としては面積図と同じになります。
・全部つるだと仮定すると、つる1匹あたりの足2本、全部の頭の数10より、2×10=20で、足の合計数は20本となります。問題文の足の合計数は32本なので、32-20=12より、12本足りません。
・そこで、足の総数が合うまで、つる1羽をかめ1匹に取り換えます。1回取り換えるごとに足の総数は、かめの足4本-つるの足2本=2本増えます。12本ふやすためには、12÷2=6より、6匹をかめに取り換えれば良いことになり、かめは6匹。
・最後に、総数10-かめ6匹=4羽より、つるは4羽です。
※このページは、小学校の先生や保護者、子ども達からのリクエストで、作成してみました。決まった解法にとらわれず、自分の得意な方法で、つるかめ算にチャレンジしていただければ幸いです。
※学習的な内容では、下記は別ページがあります
※ サイト内検索
このウェブサイトでは、快適な閲覧のために Cookie を使用しています。閲覧を続けることで、 Cookie ポリシーに同意したことになります。
本サイトに掲載のすべての画像およびWEBデータ(テキスト等)は 著作権法により保護されています。 著作権は『工房momo』サイト管理者にあり、無断で使用・転用・コピーすることは固くお断りいたします。